
Likewise, consider what happens if you invert the message (that is, you reverse the message bytewise, so that it starts with 21 and ends with 48). Both the LRC and the checksum remain unchanged! (We simply turned one bit ON in an upstream byte, and turned the same-position bit OFF downstream, creating two changes that cancel each other out at checksum time.) For example, consider the original message (“48656C6C6F20776F726C6421”) suppose we change the last two bytes of the message from 6421 to 6520. Neither checksum nor LRC can be considered robust against message corruption.
#FLETCHER CHECKSUM CALCULATOR ONLINE CODE#
If you try the code in the console using the string shown further above, you should get an answer of ’21’. We simply check for a two-nibble length, then return the final value. Since XOR never overflows, we don’t have to constrain the final result to 8 bits with an AND. In Line 6, you can see the XOR-in-place operator (^=).
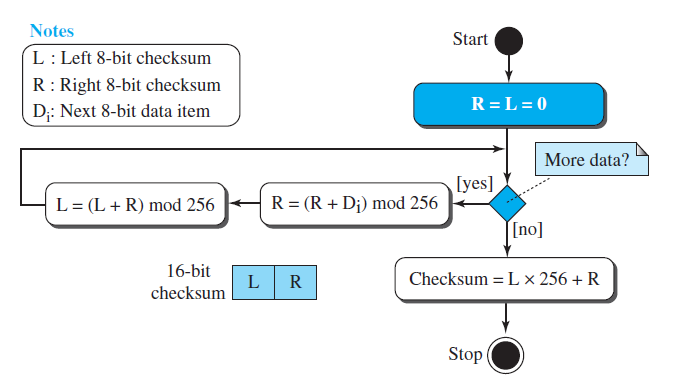
Longitudinal redundancy check (LRC) is a variation on the 8-bit checksum, differing only in that the “summation” is done using XOR, instead of numerical addition. When you hit Enter, the console should show ‘5d’ as the return value. If you want to try the code out, copy and paste the above code into your JS console (in Chrome, use Shift-Cmd-J to get the console), then add a line, at the bottom (outside the function), of CHECKSUM(“48656C6C6F20776F726C6421”). In that case, we need to prepend ‘0’ to the answer. JavaScript’s toString(16) operation returns a single-digit value for values less than 10. In Lines 10 and 11, we need to check that the final hex value is two nibbles long. At the same time, we convert back to hex using the toString() method, with an argument of 16 (meaning we want to use radix-16 or “base 16” in our final representation of the number). We do that in Line 9, with the logical-AND against 255. When we’re finished looping, we need to be sure to constrain the sum to an 8-bit value. Note that the number sum is essentially a 32-bit integer, behind the scenes, meaning our final value could be much larger than 255. We start (in Line 3) by parsing the hex input into two-nibble chunks using the regular expression /./g - which means find substrings that match the pattern “anything followed by anything” (that’s what the two dots mean), and do it globally (that’s what the ‘g’ means).” The result is an array, s, of two-digit hex values.Īt Line 5, we enter a loop (using the forEach iteration construct) in which we convert the string version of a two-nibble hex value to an actual number that we can operate on. If we use “48656C6C6F20776F726C6421” as input to the above function, the output will be “5d,” which is the hex value of the final 8-bit sum. The input to this function is expected to be a hexstring that looks something like “48656C6C6F20776F726C6421” (which, in this case, is the hex version of the ASCII string “Hello world!”). Var n = 1 * ('0x' + hexbyte) // convert hex to number The conventional 8-bit checksum is just what it sounds like: a sum of all bytes values in the input, with any overflow (from carry operations) discarded.
#FLETCHER CHECKSUM CALCULATOR ONLINE HOW TO#
Let’s take a look at how to calculate LRC, checksum, and CRC using JavaScript. But some techniques are definitely better than others. Notice, earlier, I said these data-integrity techniques can tell you whether data is “likely to have been corrupted.” No checksum technique is 100% foolproof in the general case, for arbitrary-length data. The latter isn’t really a checksum in the usual sense but is an example of a one-way hash that falls in the “linear congruential generator” family.
Three of the most popular ones are the conventional checksum, LRC (longitudinal redundancy check), and CRC (cyclic redundancy check). You’ll find a wide array of checksum techniques in common use. If so, the recipient can infer that the message probably (arguably) wasn’t altered in transit. If you add all the bytes of a message together and find (neglecting overflow) that the sum is 96, then you tack that number onto the message before sending it, the recipient can repeat your summation on the first N – 1 byte of the message, and compare the result to the final byte to see if it’s 96. Checksums of various kinds are commonly used in data communication protocols to allow the recipient of a message to determine, quickly and easily, whether the data is likely to have been corrupted in transit.


 0 kommentar(er)
0 kommentar(er)
